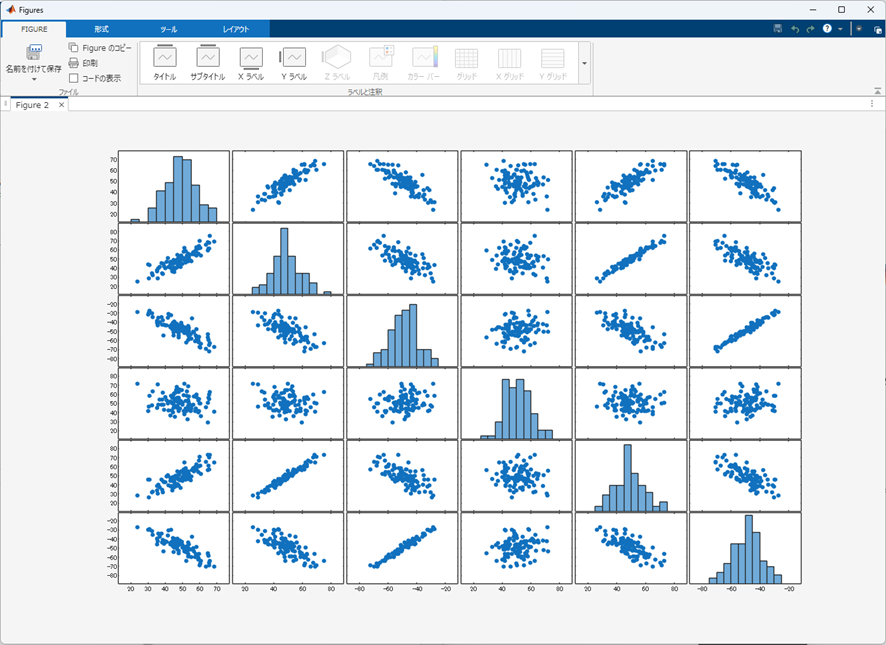
MATLABのplotmatrixという関数があります。この関数は散布図行列を作成する関数です。下図にplotmatrixで可視化した図を示します。「これは便利!」と感じる反面「調整どうやったらいいんだ…」と悩む代表格のような可視化関数でした。今回plotmatrixで可視化した図の修正方法について色々試してみたので、その内容について記載できればと考えています。
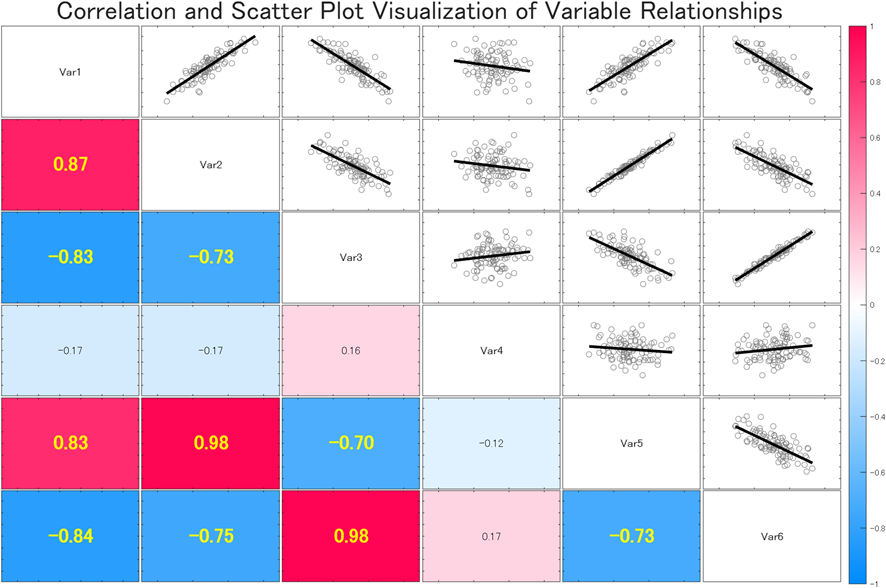
最後はこんな風に改造できました
まず、plotmatrixのすごいところ
何点かあるかと考えますが、端的にいって「手軽・便利・安心」ということでしょうか。「Tiledlayoutやsubplotで一つ一つ描いて…」という操作でできなくもないですが、表示範囲を合せたりミスなく組むのは意外にハードルがあるので素直にうれしいですね。
- 変数ごとの整合性を確認しなくていいこと
- グラフ軸の分割を気にしなくていいこと。
- 各グラフの表示範囲の整合性がとれていること
- ToolBoxが不要
plotmatrixで困ったこと
「とりあえず可視化」では便利がいいのですが、正直にいうと「調整が難しい…」と感じます。そこで、なぜ難しいと感じたかを考えてみました。今の考えとしては、「戻り値の数と種類が多くて、確かめる行為が地味に大変」なのかなと考えています。なお、公式のドキュメントでは、plotmatrixで生成される戻り値の説明は次のようになっています。

引用:https://jp.mathworks.com/help/matlab/ref/plotmatrix.html
「36個の軸と36個のグラフデータだけではなかった?」plotmatrixの中身
例えば6変数のデータをplotmatrixで可視化した際、6×6の散布図行列が表示されます。この図を最初に眺めたとき、「36個の軸と36個のグラフデータ(散布図とヒストグラム)なんだろうな…」と思っていました。ですが、この考えは思い込みだったことがわかりました。
実際に、100行×6列のサンプルデータを用意してplotmatrixで可視化してみました。そして一つ一つの戻り値の中身を確かめてみました。その結果、次のようになりました。
軸の数:
36(軸)+6(ヒストグラム軸)+1(大きな軸)
グラフデータの数:
36(lineオブジェクト)+6(ヒストグラムオブジェクト)
この数を見たとき、数がちょっと多いな…と思いました。大きな軸はともかく、lineオブジェクトが36存在し、ヒストグラムオブジェクトが6個あるのか…と思いました。
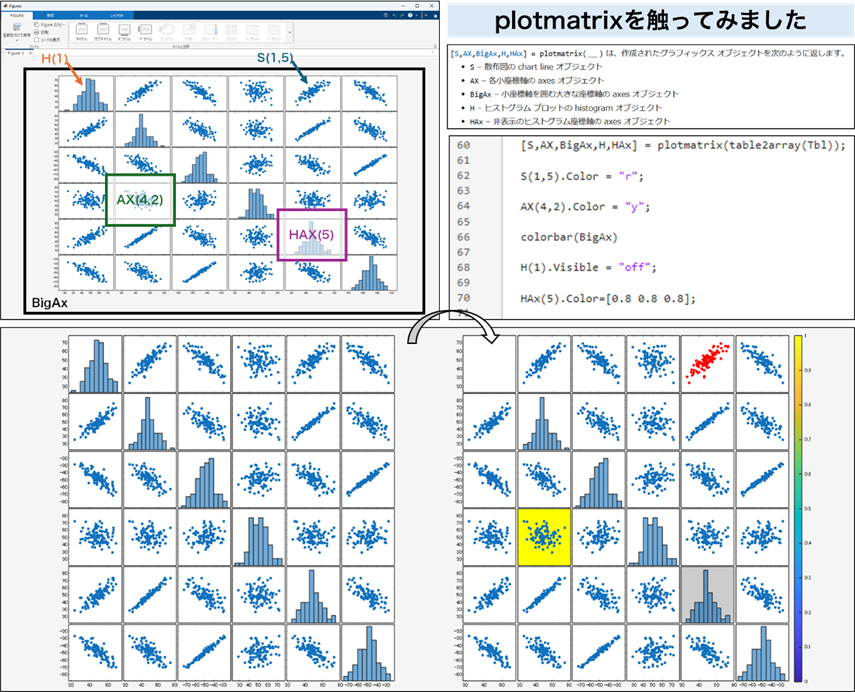
plotmatrixの戻り値の中身
色々試した結果、現状で認識できた範囲のものを図示してみました。色々と確かめた結果、「個別の枠に該当するAXや散布図のオブジェクトS」の上に「ヒストグラムのオブジェクトであるHや軸のHAXのオブジェクト」が乗っかっているイメージで納得しています。

plotmatrixの修正
戻り値の中身がわかったので、それぞれのオブジェクトで少し修正してみます。修正内容は次のようにしました。個人的に「カラーバーも出せた」のはうれしいポイントでした。
- S(散布図点):赤にする
- AX(個別の軸):黄色で軸内をぬる
- BigAx(大きな軸):カラーバーを表示する
- H(ヒストグラム):表示を消す
- HAx(ヒストグラムの軸):グレーにする
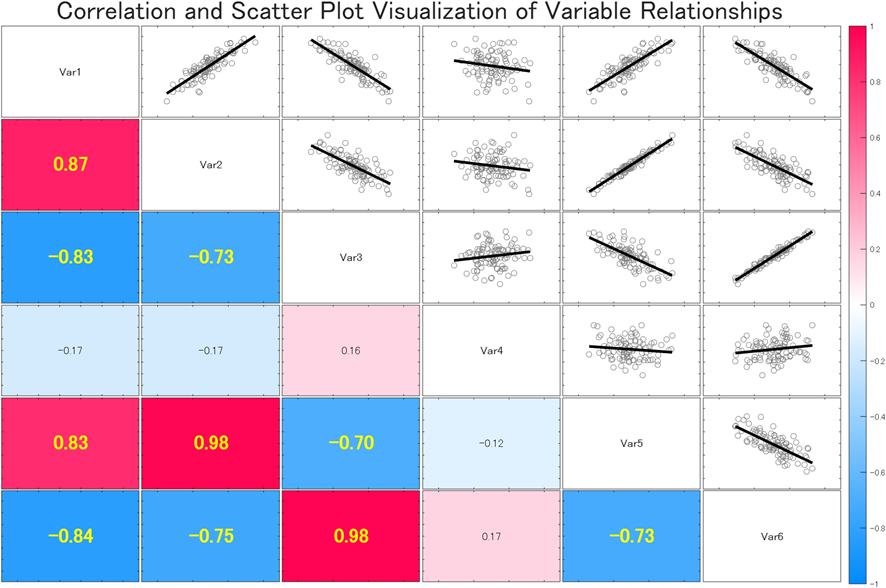
plotmatrixの改造で遊んでみる
plotmatrixで遊んでみました。勢いで作ったので、色々と怪しい部分もあるかと思います。あくまで、「見た目としてこんな調整ができるんだ」という範囲で、ご容赦いただければ幸いです。
あまり整理できていませんが、サンプルコードをブログ末に記載しています。もし、エクセルのサンプルデータが欲しいという方がいらっしゃれば、無料にてお渡しさせていただいていますので、メールやLINE、XのDMなどでご連絡いただければ幸いです。
※XのDMは相互フォローでない場合、DMが表示されないことがあります…
コンセプトです。
- テーブルデータを使用する
- テーブルの変数名を対角成分に表示する(その際ヒストグラムを消す)
- 相関係数を計算する
- 相関係数に応じて、行列の下三角領域の色を着色する(その際散布図を消す)
- 相関係数の値がしきい値以上で強調させる
- カラーバーを表示する
- 上三角成分の散布図の色などを変更し、近似直線を挿入する
- メモリラベルを削除する
SCISELでは、”MATLABやLabVIEWを使った研究・開発”のサポートや代行などを行っています。ご興味のある方はこちらまでご連絡いただければ幸いです。
clear;close all;clc
%% 読み取りと各種設定値
filename = 'Sample_Correlated_Data.xlsx';
Th = 0.5; % 蛍光色になる基準値
%% カラーマップを作成
% カラーマップのサイズ
nColors = 256;
% 3つの基準点(青 → 白 → 赤)
cx = [0, 0.5, 1];
c(1,:) = hex2rgb('#008BFB'); %マイナス側の色
c(2,:) = hex2rgb('#FFFFFF'); %中間色
c(3,:) = hex2rgb('#FF0051'); %プラス側の色
% 補間用のx座標
xq = linspace(0,1,nColors);
% 各色成分をinterp1で補間
r = interp1(cx, c(:,1), xq);
g = interp1(cx, c(:,2), xq);
b = interp1(cx, c(:,3), xq);
% カラーマップを結合
CustomColormap = [r' g' b'];
climValue = [-1 1];
%% テーブルデータの読み取りと変数名を参照
Tbl = readtable(filename);
varName = Tbl.Properties.VariableNames;
%% 相関行列の計算と可視化
R = corrcoef(table2array(Tbl));
data = tril(R);
Idx = abs(data) > Th;
%% 相関係数に基づく色の割付(カラーインデックスの計算)
dataValue = R;
% 正規化して 1〜256 のインデックスに変換
nColors = size(CustomColormap, 1);
normalizedValue = (dataValue - climValue(1)) / (climValue(2) - climValue(1));
normalizedValue = min(max(normalizedValue, 0), 1); % 0〜1 にクリップ
% インデックス取得(1〜nColors)
colorIndex = round(1 + (nColors - 1) * normalizedValue);
%% 散布図行列の調整
figure
[S,AX,BigAx,H,HAx] = plotmatrix(table2array(Tbl));
% BigAx.PlotBoxAspectRatio=[3 3 3];
% タイトルを表示
title(BigAx,"Correlation and Scatter Plot Visualization of Variable Relationships",FontSize=24)
% カラーマップの設定
colormap(BigAx,CustomColormap);
clim(BigAx,[climValue(1) climValue(2)])
colorbar(BigAx)
% 散布図の数(列数)
n = width(Tbl);
% 各散布図に対して処理を実施
for i = 1:n
for j = 1:n
if i==j % 対角成分の調整
H(1,i).Visible="off";
% HAx(1,i).Color=[0.8 0.8 0.8];
axh=HAx(1,i);
ax = AX(i,j);
text(axh, 0.5, 0.5,varName(i), ...
'Units', 'normalized', ...
'HorizontalAlignment', 'center', ...
'VerticalAlignment', 'middle', ...
'FontSize', 10, ...
'Color', 'k',...
'FontWeight', 'bold',...
'Interpreter','none'); % 文字色(必要に応じて)
end
if i < j % 上三角側の調整
ax = AX(i,j); % 対応する軸を取得
axes(ax); % 現在の軸に設定
% x: 第j変数, y: 第i変数
% x = table2array(Tbl(:,j));
% y = table2array(Tbl(:,i));
x = S(i,j).XData;
y = S(i,j).YData;
% 欠損値除去(NaNがある場合)
valid = ~(isnan(x) | isnan(y));
x = x(valid);
y = y(valid);
% 線形近似(1次)
p = polyfit(x, y, 1);
yfit = polyval(p, x);
% 回帰直線を重ねる
hold on;
S(i,j).MarkerSize=5;
S(i,j).Marker="o";
S(i,j).Color=[0.5 0.5 0.5];
plot(x, yfit,'-', 'Color','k','LineWidth', 2.5);
hold off;
end
if i>j % 下三角側の調整
S(i,j).Visible = "off";
viewValue=sprintf('%.2f',dataValue(i,j));
ax=AX(i,j);
if Idx(i,j)==1
% 強調時のテキスト表示
text(ax, 0.5, 0.5,viewValue, ...
'Units', 'normalized', ...
'HorizontalAlignment', 'center', ...
'VerticalAlignment', 'middle', ...
'FontSize', 18, ...
'Color', 'y',...
'FontWeight', 'bold',...
'Interpreter','none');
else
% 通常時のテキスト表示
text(ax, 0.5, 0.5,viewValue, ...
'Units', 'normalized', ...
'HorizontalAlignment', 'center', ...
'VerticalAlignment', 'middle', ...
'FontSize', 10, ...
'Color', 'k',...
'FontWeight', 'normal',...
'Interpreter','none');
end
% 相関係数の値に応じて色を塗る
AX(i,j).Color=CustomColormap(colorIndex(i,j), :);
end
% メモリラベルを消す
xticklabels(ax,{})
yticklabels(ax,{})
end
end
% daspect(BigAx,[1 1 1])
